The Drivers of Prescription Drug Expenditures – A Methodological Report

ISBN: 978-1-100-22990-4
Cat. No.: H82-15/2013E-PDF
December 2013
PDF version
Executive Summary
Prescription drug expenditures represent a significant component of health care costs in Canada, with estimates of $27.7 billion spent in 2012. After several years of double-digit growth, the rates of change in these expenditures have gradually declined in recent years, forecasted at a 16-year low for 20121.
Changes in prescription drug expenditures are driven by many factors. For example, while the recent rate decline has mainly been driven by the launch of generic products and generic price reforms, expensive emerging therapies, as well as increases in the volume of drug use, are expected to continue to fuel the upward pressures on costs.
Given the complex forces at work, simple statistics on drug utilization and costs only provide a limited insight into the factors that drive growth. Identifying the major drivers and understanding the effect they have on prescription drug expenditures allows policy makers and researchers to anticipate future cost pressures and expenditure levels.
This methodological report (i) describes the factors that drive prescription drug expenditures; (ii) discusses the data requirements and approaches to the analysis; and (iii) provides the methodology and formulas required to decompose the change in prescription drug expenditures and measure its drivers.
The tri-layer approach provides (i) high-level policy decision makers with a broad understanding of the factors driving drug expenditures; (ii) researchers interested in understanding cost driver analyses with a description of the basic mechanics of this method; and (iii) researchers setting out to conduct actual cost driver analyses with the complete methodology and formulas.
Drivers of prescription drug expenditures
This report discusses the drivers of the two components of prescription drug expenditures: drug costs and dispensing fees.
Drivers of Drug Costs
The drivers of drug costs are grouped in four broad categories of effects. Each effect captures the impact of the change in the corresponding driver:
- Price Effects
- Price Change Effect – changes in the price of both brand-name and generic products
- Generic Substitution Effect – shifts from brand-name to generic products
- Volume Effects
- Prescription Volume Effect – shifts in the number of prescriptions dispensed to patients
- Prescription Size Effect – shifts in the average number of units per prescription
- Strength–Form Effect – shifts in the use of strengths or formulations of a molecule
- Drug Mix Effects
- Existing Drug Effect – shifts in utilization among drugs available in both periods analyzed
- Exiting Drug Effect – shifts in utilization from drugs that have exited the market in the second time period
- Entering Drug Effect – shifts in utilization from existing drugs towards drugs that have entered the market in the second time period
- Demographic Effects
- Population Effect – shifts in the number of people utilizing drugs
- Aging Effect – shifts in the distribution of the population across age groups
- Gender Effect – shifts in the distribution of the population by gender
While these effects account for the changes in drug cost, they may be influenced by factors that are not easily measured. These include disease prevalence, prescribing practices and socio-economic factors.
Drivers of Dispensing Fees
In addition, the report identifies three drivers of dispensing fees:
- Fee Effect – shifts in dispensing fees
- Prescription Size Effect – shifts in the average number of units per prescription
- Drug Volume Effect – changes in the number of units dispensed
The Demographic Effects listed above can also be calculated for the dispensing fees portion of the prescription drug expenditures.
Basic approach
The methodology proposed in this report uses the Laspeyres approach to decompose cost into two determinants or factors: price and quantity. By comparing two time periods, this approach isolates the effect of the change in a specific factor (e.g., price) by holding the other factor (e.g., quantity) constant at the base-period value.
The many factors that drive prescription drug expenditure can be isolated and quantified by expanding the Laspeyres approach to a multi-factorial framework.
Data requirements
In this type of framework, in addition to basic price and quantity information, drug-related information is required for each of the two time periods being compared (e.g., molecule name, strength, form, brand–generic type, etc.). If available, demographic information can be incorporated into the methodology.
These data elements may be available in administrative databases with information on drugs shipped, sold, dispensed or reimbursed in Canada. These include private and public drug plan data, pharmacy sales data, drug shipment data, hospital data etc. These data sets can be used to tease out the drivers of prescription drug expenditures based on the proposed methodology.
Formula
The report provides a detailed technical section that includes a discussion of the methodology and step-by-step demonstrations of how the formulas were derived. For each effect, the mathematical formula is provided.
Recognizing that there may be more than one way to conduct a cost driver analysis depending on the purpose and analytical depth of the research and data availability, the report also discusses how the proposed methodology can be adjusted and enhanced.
Detailed discussions of the methodology and formulas for the residual Cross Effects are provided in the Appendixes.
Acknowledgements
This report was prepared by the Patented Medicine Prices Review Board (PMPRB) under the provisions of the National Prescription Drug Utilization Information System (NPDUIS).
The PMPRB would like to acknowledge the contributions of:
- The members of the NPDUIS Steering Committee, for their expert oversight and guidance in the preparation of this report.
- The Canadian Institute for Health Information for reviewing and commenting on the methodology proposed in this report.
- Dr. Steve Morgan, for reviewing and providing expert advice on the methodology proposed in the report.
- The PMPRB NPDUIS staff for their contribution to the analytical content of the report: Elena Lungu, A/Manager NPDUIS; Orlando Manti, Manager Economics; and the PMPRB scientific and editing groups.
Disclaimer
NPDUIS is a research initiative that operates independently of the regulatory activities of the Board of the PMPRB. The statements and opinions expressed in this NPDUIS report do not represent the official position of the PMPRB.
1 CIHI. 2013. Drug Expenditure in Canada, 1985 to 2012. Ottawa: Canadian Institute for Health Information. https://secure.cihi.ca/free_products/Drug_Expenditure_2013_EN.pdf
1.Introduction
Prescription drug expenditures represent a significant component of health care costs in Canada, with approximately $27.7 billion spent on prescription medication in 2012. After several years of double-digit growth, the rates of change in these expenditures have gradually declined in recent years, with a 16-year low forecasted for 2012 (CIHI 2013).
Factors – The level of prescription drug expenditures is determined by many factors or determinants, such as the size and the age of the population, the volume and the type of drugs being used, the price levels, etc.
Drivers – A change in any factor becomes a cost driver. For example, the changes in the brand versus generic market shares due to the launch of generic products are expected to drive a decline in the rate of growth in prescription drug expenditures. On the other hand, expensive emerging therapies are expected to fuel the upward pressures on costs.
Effects – Intuitively, it is expected that these cost drivers would result in changes in the level of prescription drug expenditures. Measuring the precise impact of a driver on these levels is done by determining its effect. When comparing two time periods, the effect on expenditures can be calculated by allowing one factor to change and holding the other factors constant at their base-period values.
Given the complex forces at work, simple statistics on drug utilization and costs only provide a limited insight into the factors that drive growth. Identifying the major drivers and understanding the effect they have on prescription drug expenditures allows policy makers and researchers to anticipate future cost pressures and expenditure levels. Previous studies have been published discussing the factors contributing to the growth in health care costs (CBO 2008; CIHI 2011) and, more specifically, to the growth in drug costs (Morgan 2002, 2004, 2005; Gerdtham and Ludin 2004; CIHI 2012).
This methodological report builds on the previously published work, including that of the PMPRB (PMPRB 2004, 2006, 2011), and the proposed approach was developed in consultation with the Canadian Institute for Health Information (CIHI).
This report provides the tools required for a complete analysis of the drivers of prescription drug expenditures by
- describing the drivers and the effect they have on prescription drug expenditures (Section 2);
- discussing the data requirements and approaches to the analysis (Section 3); and
- providing the methodology and formulas required to decompose prescription drug expenditures and conduct cost driver analyses (Section 4).
In this report, the drivers of the two major components of prescription drug expenditures – drug costs and dispensing fees – are analyzed in the context of four broad categories: Price Effects, Volume Effects, Drug-Mix Effects and Demographic Effects. Each of these categories is further divided into more specific effects. This report provides formulas for all of the individual effects, as well as for the residual cross effects.
The methodology is not limited to trend analyses of changes in sales or expenditures over time, but can also be employed in cross-jurisdictional analyses or international comparisons that break down the sources of differences in drug sales or expenditures. Furthermore, using the standard methodology, it is possible to conduct specialized analyses in particular therapeutic classes or market segments.
The proposed methodology can be used with a broad array of administrative databases including private and public drug plan data, pharmacy sales data, drug shipment data and hospital data. It can be adjusted and enhanced based on data availability as well as the purpose and analytical depth of a particular research study (Section 5).
Depending on the source of the information, the available data may not explicitly account for all drivers, such as disease prevalence, prescribing practices, and socio-economic factors. For example, cost driver analysis can determine the extent to which a change in expenditure is due to increasing use, but cannot quantify what part of the increase in utilization is attributable to marketing activities. The proposed methodology has a number of limitations, which are detailed in this report (Section 6).
In-depth discussions of the methodology and the formulas are provided in the appendixes.
2.Overview of the Drivers of Prescription Drug Expenditures
Prescription drug expenditures generally have two distinct components: the drug cost and the dispensing fee. The drug cost is the actual cost of the medication and may include wholesale upcharges and/or pharmacy markups. The dispensing fee is a fee for service charged by the pharmacist when dispensing a prescription.
Although these are two different types of expenditures (price of drugs versus fees for services), their growth may be driven by some of the same factors, such as changes in the size of the population, aging and the volume of prescriptions.
Generally, cost driver analyses focus on the actual drug costs, which usually represent the largest component of prescription drug expenditures (Morgan 2002, 2004, 2005; Gerdtham and Ludin 2004; PMPRB 2004, 2006). Nevertheless, cost driver models have also been applied to dispensing fees (PMPRB 2011), as they can represent a significant portion of the costs.
This section provides an overview of the effects that can be extracted using the proposed methodology. Each effect captures the impact of a specific driver on the level of prescription drug expenditures.
Section 2.1 discusses the drivers of drug costs, Section 2.2 discusses the drivers of dispensing fees and Section 2.3 discusses the drivers of the plan-paid share of costs. The cross effects are discussed in Section 2.4.
Note that the cost driver analysis is not limited to the effects discussed nor does it necessarily encompass all of these effects. The Methodology Adjustments and Enhancements section (Section 5) describes how the approach may be adapted depending on the availability of data and specific research needs.
2.1 Drivers of Drug Costs
The drivers of drug costs may be grouped into four broad categories: Price Effects, Volume Effects, Drug-Mix Effects and Demographic Effects. Each effect captures the impact of a change in a specific factor. A description of the individual effects follows.
Price Effects
1. Price Change Effect
This effect captures the impact of changes in drug prices and is determined at the strength, form, and brand-name or generic level. For instance, the recent generic price reforms that resulted in lower generic prices have a negative price change effect on drug costs.
2. Generic Substitution Effect
This effect captures the impact of shifting utilization from higher cost brand-name products to lower cost generic products. This effect is expected to have negative values when generic products are launched.
Volume Effects
3. Prescription Volume Effect
This effect captures the impact of changes in the number of prescriptions dispensed to a standardized patient population over the two time periods analyzed. There are many factors that may influence this effect, including the multiple use of drugs, the presence of comorbidities, the persistency of treatment and prescribing practices, among other things. Moreover, in the absence of demographic information, the Prescription Volume Effect also captures the aging of the population and changes in the gender split, as well as changes in the size of the population using the drugs.
4. Prescription Size Effect
This effect captures the impact of changes in the average number of units of a drug dispensed per prescription. An increase in this measure contributes positively to the increase in drug costs, unless it is offset by a reduction in the number of prescriptions (i.e., Prescription Volume Effect).
5. Strength – Form Effect
This effect captures the impact of shifting utilization towards different strengths or formulations of a molecule (active ingredient). Drugs are typically available in a variety of strength–form combinations for which the cost per unit can vary substantially. An increase in the use of the higher strength of drugs could contribute positively to the drug cost growth, as, generally, higher strengths are more expensive than the lower strengths.
Drug-Mix Effects
6. Existing Drug Effect
This effect captures the impact of shifts in market shares between molecules (active ingredients) that are available in both time periods analyzed. This important driver may reflect changing treatment patterns, physician prescribing practices and/or the prevalence of diseases in the population. This effect captures switching between drugs, as well as the shifts in market shares among the various therapeutic classes and subclasses. The proposed methodology can differentiate between these components by further decomposing this effect into therapeutic class and subclass level, as detailed in Section 5 of this report.
7. Exiting Drug Effect
This effect captures the impact of shifts in utilization away from drugs that are no longer utilized in the second time period. Its contribution is expected to be minimal, unless important drugs are withdrawn (e.g., Vioxx).
8. Entering Drug Effect
This effect captures the impact of shifts in utilization towards drugs that have entered the market in the second time period. With new drugs constantly being launched, this may be an important cost driver. Less expensive new drugs will offer savings and more expensive new drugs will result in cost increases. The value of this driver will represent the net effect of these two opposing forces.
Demographic Effects
If demographic information is available in the data, the demographic components may be isolated from the general Prescription Volume Effect. These drivers can influence both drug costs and professional fee expenditures. Section 4 of the report discusses the Demographic Effects of both the drug costs and dispensing fees.
9. Population Effect
This effect captures the extent to which the incremental change in the size of the population contributes to changes in drug costs or dispensing fees.
10. Aging Effect
This effect captures the impact of changes in the distribution of the population by age groups. An older population is generally associated with increased drug use and cost. Therefore, population shifts toward an older or a younger population impacts the growth of prescription drug expenditures in a positive or negative way, respectively. Note, however, that unless major changes occur in the population (e.g., the introduction of a new drug plan), this effect should have a minimal impact on year-over-year cost, and it may only show a notable impact over a longer time period (e.g., 5 or 10 years).
11. Gender Effect
This effect captures the impact of changes in the gender split in the population. Drug costs may differ depending on gender due to differences in disease prevalence and drug utilization patterns. Like the Aging Effect, unless major changes occur in the population, this effect should be minimal and may be grouped with the above effect into an Aging–Gender Effect.
2.2 Drivers of Dispensing Fees
This section identifies three drivers of dispensing fees. A similar methodology and results on the drivers of professional fee expenditures were published in a previous NPDUIS report (PMPRB 2011).
1. Fee Effect
This effect captures the impact of changes in the average cost of dispensing fees.
2. Prescription Size Effect
This effect captures the impact of changes in the average number of units of a drug dispensed per prescription. Note that this effect is also driving drug costs, but has the opposite result of that discussed in Section 2.1. An increase in this measure contributes negatively to the increase in dispensing fees, as fewer prescriptions are required to dispense a constant quantity of drugs.
3. Drug Volume Effect
This effect captures the impact of changes in the number of units of a drug dispensed to patients over the two periods analyzed.
Note that if 'day supply' information is available and reliably reported in the data, it may replace the 'unit' information when calculating the drivers of dispensing fees. In this case, the Prescription Size Effect and the Drug Volume Effect will become the Prescription Length Effect and a Volume Effect that reflects day supply information.
If demographic information is available in the data, the demographic components may be isolated from the general Drug Volume Effect, and the three demographic effects listed above can also be calculated for the dispensing fee component of prescription drug expenditure.
2.3 Drivers of Plan-Paid Share of Costs
In addition to information on drug costs and dispensing fees, some administrative databases may contain information on the portion of prescription drug expenditures reimbursed by drug plans (public or private), as well as the remaining portion paid by the beneficiary. This report also discusses the drivers of plan-paid and beneficiary-paid amounts.
2.4 Cross Effects
Individual effects derived using the methodology proposed in this report explain most, but not all, of the changes in prescription drug expenditure. This is because the effect of each factor is determined by assuming that all the other factors remained unchanged over the period analyzed. In reality though, multiple factors change simultaneously, creating residual or cross effects.
Cross effects may be reported separately or they may be distributed across the individual effects. A detailed discussion is provided in Section 3. The greater the number of individual effects, the more cross effects will result from their interaction.
The existence of cross effects does not represent a deficiency in the standard cost-driver framework, but it is the irreducible result of interactions among changes in the inputs.
3. Basic Requirements and Approaches
Undertaking cost driver analyses requires an understanding of the basic mechanics of the methodology: what is required to make it work and how it works. Section 3.1 discusses the required sources of data and data elements. Section 3.2 discusses the underlying logic of the Laspeyres index in the proposed methodology. Section 3.3 discusses the alternative approaches of the Paasche and the Fisher ideal decomposition.
3.1 Data Requirements: Sources and Data Elements
Sources
Administrative databases with information on drugs shipped, sold, dispensed or reimbursed in Canada can be used to tease out the cost drivers. These include private and public drug plan data, pharmacy sales data, drug shipment data, hospital data etc. These databases generally contain information on the drugs and quantity, measures of price and/or costs, and some demographic information.
Many of the databases also include the Drug Identification Number (DIN) issued by Health Canada. If the DIN is available, data can be linked across databases and with the Health Canada Drug Product Database (DPD)1. The DPD contains very detailed product-specific information on drugs approved for use in Canada including the trade name, molecule/ingredient name, strength, form, packaging, manufacturer, therapeutic classification etc.
A thorough understanding of the available databases and their limitations is required for a successful analysis. The quality of the data needs to be verified and ensured before analyzing and reporting the results. In addition, an expertise in data analysis and a familiarity with the software used to analyze large data sets are required.
Data Elements
To conduct cost driver analyses, the following basic data elements are required for each of the two time periods being compared: (i) information on the individual drugs; (ii) the quantity and corresponding market shares of individual drugs; and (iii) corresponding drug costs or prices. If available, demographic information can be incorporated in the methodology to enhance the understanding of the factors that drive costs.
Drug Information
Drug information includes a broad array of attributes such as the DIN, trade name, molecule/ingredient name, strength, form, package size, therapeutic class and subclass, manufacturer, and whether the drug is a brand-name or generic, among other things. The methodology proposed in this study requires the drug information at the following level: molecule/ingredient name, strength, form and brand–generic flag.
Quantity
Drug quantity can be measured in various ways: the number of prescriptions, physical units or treatment days.
The number of prescriptions is a broad measure of the quantity of drug use. While it has the advantage of being cumulative across drugs, it has the disadvantage of concealing the true volume of the physical units (prescription size) as well as the unitary price/cost of the drugs (price of drugs). Therefore, although it has been used as a standalone measure of quantity in cost driver analyses, the number of prescriptions is generally used in conjunction with the number of physical units.
The number of physical units identifies the price/cost at a unit level as well as the average number of units per prescription. Without information on the number of prescriptions, physical units are not a useful standalone measure of quantity. The numbers of units are generally not cumulative across drugs, given that drugs come in different formulations (oral solids, injectable, ointments, patches, etc.)
The number of treatment days (or day supply) may be available in some administrative databases and can be employed in the cost decomposition methodology to include a treatment intensity or length component. However, the reliability and consistency of the reporting of this data needs to be assessed before it is used.
The World Health Organization Defined Daily Dose (DDD) has also been used to decompose drug spending increases (Gerdtham and Lundin 2004). However, previous studies have advised using caution when interpreting the average cost or price at the DDD level (PMPRB 2010).
Price or Cost
This can include various measures of prescription drug sales or costs: drug prices at various sale points (manufacturer, wholesaler, pharmacy) or drug costs reimbursed by drug plans. These may reflect wholesale upcharges and pharmacy mark-ups.
The expenditures associated with dispensing fees at the prescription level may also be analyzed in a cost driver analysis (PMPRB 2011).
Demographic Information
Some administrative databases (for example public or private drug plan data) may collect demographic information, such as the number of people using the drugs over the two time periods, as well as their age and gender. Cost driver analyses can incorporate this high-level demographic information.
3.2 The Basic Cost Decomposition
The cost driver methodology proposed in this report uses the Laspeyres approach to decompose cost into two determinants or factors: price and quantity. This method has been used in other PMPRB studies of prescription drug expenditures (PMPRB 2004, 2006 and 2011).
The basic principle underlying cost decomposition is applicable to many areas of economic analysis. There is extensive literature on price and quantity indexes and how expenditure can be divided into a price and a quantity component (Berndt et al. 2000; Diewert 2001; United Nations Statistics Division 2008).
By comparing two time periods, the Laspeyres approach isolates the effect of the change in a specific factor (e.g., price) by holding the other factor (e.g., quantity) constant at the base-period value. The many factors that drive prescription drug expenditure can be isolated and quantified by expanding this approach to a multi-factorial framework.
This section discusses the Laspeyres index and describes the simple model of one product and two factors: price and quantity. The next section discusses alternative approaches, namely the Paasche index and the Fisher ideal index. A more detailed discussion of these three indexes is provided in Appendix 1, 2 and 3, respectively.
Basic Cost Decomposition using the Laspeyres approach
Suppose some monetary variable X (e.g., drug expenditure) is the product of a price P and the measure of physical quantity Q. In algebraic terms:
(1) X = PQ
Suppose as well that we have observations of X, P and Q for two periods, a current period (denoted by the index number "1") and a base period (denoted by the index number "0"). It follows from (1) that:
(2.1) X(0) = P(0)Q(0)
(2.2) X(1) = P(1)Q(1)
Suppose, finally, that we are interested in knowing what part of the change in X that occurred between the base period and current period can be attributed to each of P and Q. One approach begins by noting that current-period price (or quantity) equals its base-period counterpart plus the change in price (or quantity) that occurred between the two periods:
(3.1) P(1) = P(0) + [P(1) – P(0)]
(3.2) Q(1) = Q(0) + [Q(1) – Q(0)]
Substituting (3.1) and (3.2) into (2.2) gives:
(4) X(1) = {P(0) + [P(1) – P(0)]} {Q(0) + [Q(1) – Q(0)]}
Expanding the right-hand side of (4) gives:
(5) X(1) = P(0)Q(0)
+ [P(1) – P(0)]Q(0)
+ P(0)[Q(1) – Q(0)]
+ [P(1) – P(0)] [Q(1) – Q(0)]
Subtracting X(0) from both sides of (5) while noting (2.1) gives:
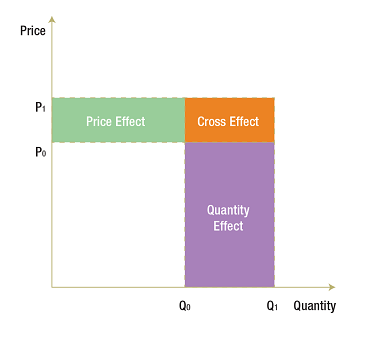
(6) X(1) – X(0) = [P(1) – P(0)]Q(0) (Price Effect)
+ P(0)[Q(1) – Q(0)] (Quantity Effect)
+ [P(1) – P(0)] [Q(1) – Q(0)] (Cross Effect)
The three terms on the right-hand side of (6) constitute one possible decomposition of expenditure change.
Price Effect: The first term on the right-hand side of (6) is referred to as the price effect and is a Laspeyres2 type of price index expressed as a difference rather than in a ratio form. This measures the impact on X of the change in price that occurred between the base period and current period, with the impact evaluated at the base-period quantity Q(0). It employs a forward-looking approach by providing an exact answer to the question:
How much would X have changed between the base period and the current period had price changed but not quantity?
Quantity Effect: The second term on the right-hand side of (6) is referred to as the quantity effect and it is a Laspeyres type of quantity index expressed as a difference rather than in a ratio form. This measures the impact on X of the change in quantity that occurred between the base period and the current period, with the impact evaluated at the base-period price P(0). It employs a forward-looking approach by providing an exact answer to the question:
How much would X have changed between the base period and the current period had quantity changed but not price?
Cross Effect: The third term on the right-hand side of (6) has a different form than the price and quantity effects, in that it involves changes in both P and Q. This is usually called the “Laspeyres cross effect” and measures the impact on X of the interaction between the change in price and the change in quantity. The cross effect is distinct from the price and quantity effects and must be included if the decomposition is to fully account for the change in X.
The following diagram illustrates the price, quantity and cross effects. In the base period, with price at P(0) and quantity at Q(0), expenditure is represented by the white rectangle. The price rises from P(0) to P(1) and quantity from Q(0) to Q(1) in the current period. The corresponding increase in X is represented by the coloured areas. The green rectangle represents the price effect (i.e., the impact on X of the change in price evaluated at Q(0)). The purple rectangle represents the quantity effect (i.e., the impact on X of the change in quantity evaluated at P(0)). The orange rectangle, with the base [Q(1) – Q(0)] and the height [P(1) – P(0)], completes the expenditure change area. This last rectangle represents the cross effect (i.e., the impact on X of the interaction between the change in prices and the change in quantity).
The Laspeyres decomposition discussed above describes the simple case of one product for which the expenditure is a function of two factors: price and quantity. Real-world cost driver analysis typically encompasses many products for which the drug expenditure is a function of multiple factors. This type of framework is discussed in detail in Appendix 1.
3.3 Alternative Approaches
While this study proposes an approach based on the Laspeyres decomposition, there are other valid approaches that may be employed in cost driver analyses, such as the Paasche or the Fisher ideal indices. These price and quantity indices have their own limitations, and the choice of approach should depend on the focus of the research as well as the proposed application of the results. A brief review of the three approaches follows.
Laspeyers approach
As discussed, the Laspeyers approach is forward-looking, evaluating each cost driver by holding the other factors at their base-period values. It should be employed to answer the following type of question:
How much higher is the expenditure this year simply because of higher prices?
This approach should be employed when the price and the quantity effects need to reflect the actual overall increase in prices and in quantity, respectively, i.e., considering the cross effect separately. (For a more detailed description, see Appendix 1.)
Paasche approach
In contrast, the Paasche approach is backward-looking, evaluating each cost driver by holding other factors at their current-period values. It should be employed to answer the following type of question:
How much lower would the expenditure have been this year at last year's prices?
This approach may be used in conjunction with the Laspeyres approach in the Fisher ideal decomposition. (For a more detailed description, see Appendix 2.)
Fisher ideal approach
The Fisher ideal approach is a hybrid of the forward-looking Laspeyres approach and the backward-looking Paasche approach. The Fisher ideal decomposition, unlike the Laspeyres approach, does not break out the cross effects separately, rather it distributes them equally among the individual contributing drivers. Thus it is considered to be a full-attribution of expenditure approach. The same result can be achieved by equally distributing the Laspeyres cross effects across the individual factors. (See the algorithm outlined in Appendix 4.)
The Fisher ideal approach fully attributes expenditures to the individual effects; thus, each effect captures the interaction with all the other effects. This approach should only be employed when the equal distribution of the cross effects is considered appropriate.
Equally distributing the cross effects may be viewed as arbitrary, but it is no less arbitrary than assigning a cross effect entirely to one driver. One could go further and argue that this approach has the appealing property of impartiality: in the absence of any strong grounds for assigning a greater amount of the cross effect to one driver or another, an equal split between the two seems appropriate.
If the drivers of expenditure change independently of one another, then it is reasonable to assume that the cross effects should be divided equally. However, this is not always the case. Let's assume, for instance, that the quantity of drugs has increased only because of the launch of a generic drug and the price discount it offers. If the intent is to fully attribute the cross effect to the quantity effect and the generic substitution effect, then arguably it should be assigned to the latter in its entirety. In such a case, the generic substitution effect will not only reflect the generic price discount (expected to be a negative effect) but will also reflect the increase in utilization (expected to be a positive effect). The net effect will be positive or negative depending on which impact is the greatest.
What if there were three factors to consider? Suppose, for example, that a model was considered in which expenditure was a function of the product of price, quantity-per-claimant and claimant population. In this case there would be four Laspeyres cross effects to compute: three double effects involving changes in two of the three factors, as well as a triple effect involving changes in all three factors. The Fisher ideal decomposition approach requires that we divide each double cross effect equally between the two factors contributing to the change. Similarly, the triple cross effect should be divided equally among all three factors.
In a complex multi-factorial cost decomposition methodology, such as the one proposed in this study, there will be a large number of interactions between the individual factors, corresponding to double, triple, quadruple, etc. cross effects. A discussion of these cross effects along with the corresponding formulas is provided in Appendixes 4–8. The equal distribution of these cross effects across the individual factors to achieve full attribution can be a very complex exercise.
Thus, the Laspeyers approach is recommended. In this case, the individual effects will be reported as described in the next section (Section 4) and the change in expenditure that is left unexplained due to the cross effects will be reported separately.
1 http://www.hc-sc.gc.ca/dhp-mps/prodpharma/databasdon/index-eng.php
2 The designation “Laspeyres” comes from the well-known the Laspeyres price index methodology. Perhaps the leading example of a Laspeyres price index is the Consumer Price Index. The Laspeyres methodology assesses the general tendency in prices by tracking the cost of a fixed “basket” of items over time.
4. Formulas for Calculating the Drivers of Prescription Drug Expenditures
This section provides the formulas for calculating the drivers of prescription drug expenditure, along with the data requirements and the methodological notes that can be applied to quantify the drivers of drug costs (Section 4.1) and the drivers of dispensing fees (Section 4.2). Section 4.3 provides the formulas required to determine the Demographic Effects for both drug costs and dispensing fees. The final section (Section 4.4) considers the drivers of the plan-paid share of costs.
As previously discussed, the proposed methodology is conceptually based on the Laspeyres approach to cost decomposition. The analysis may be limited to this approach and the cross effects reported separately. Alternatively, the Fisher ideal approach may also be employed by fully attributing the Laspeyres cross effects to the individual factors. The algorithm outlined in Appendix 4 provides the framework for this.
4.1 Drivers of Drug Costs
The drivers of drug costs are identified below in the context of three broad categories, as defined in Section 2.1.
Price Effects:
- Price Change Effect
- Generic Substitution Effect
Volume Effects:
- Prescription Volume Effect
- Prescription Size Effect
- Strength–Form Effect
Drug-Mix Effects:
- Existing Drug Effect
- Exiting Drug Effect
- Entering Drug Effect
As a minimum, the following data elements are required for two time periods:
blankblank
| Molecule (active ingredient) |
|
| Brand–generic flag |
Drug Attributes |
| Strength and form3 |
|
blank
| Drug costs, sales or drug prices |
|
| Units (number of tablets, capsules, etc.) |
Metrics |
| Number of prescriptions |
|
The metrics are aggregated at the attribute level, as opposed to the DIN level, to eliminate unnecessary detail, such as packaging sizes and manufacturer information.
In addition, all molecules need to be assigned an existing–exiting–entering status based on whether they were utilized in both the time periods compared:
- Existing Drugs – molecules were utilized in both periods
- Exiting Drugs – molecules were utilized in the first period but not in the second period
- Entering Drugs – molecules were not utilized in the first period but were utilized in the second period
Grouping the molecules by existing–exiting–entering status should be based on their actual utilization as observed in the data, as opposed to the Notice of Compliance date, launch date, formulary date or any other date.
Note that in the context of this analysis, a product refers to any unique combination of the following attributes: strength–form combination (s), brand–generic flag (b), molecule (m) and existing–exiting–entering status (e).
The drug costs or sales for a multi-product market in a given time period can be written as the product of the average cost per unit, average number of units per prescription and the number of prescriptions for a product, summed up over all products:
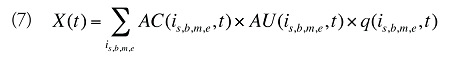
where
is,b,m,e is a product of a certain strength–form combination (s), brand–generic flag (b), molecule (m) and existing–exiting–entering status (e)
t is a constant value corresponding to the time period analyzed
X(t) is the total drug expenditure or sales in time period t
AC(is,b,m,e,t) is the average cost or price per physical unit for product is,b,m,e in time period t
AU(is,b,m,e,t) is the average number of units (physical quantities) per number of prescriptions for product is,b,m,e in time period t
q(is,b,m,e,t) is the number of prescriptions for product is,b,m,e in time period t
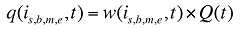
where
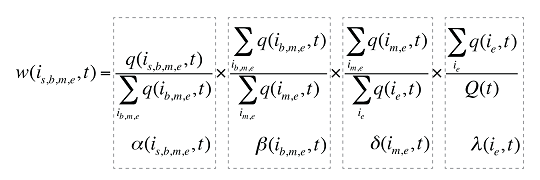
w(is,b,m,e,t) is the product's is,b,m,e share of total volume (expressed in prescriptions) in time period t
Q(t) is the total number of prescriptions in time period t
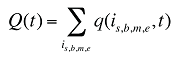
(8)
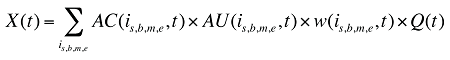
Each individual share w(is,b,m,e,t) can be decomposed into multiple shares, as follows:
(9)
where
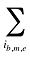 is the sum of the quantity of prescriptions for all products i with the same brand–generic flag (b), molecule (m) and existing–exiting–entering status (e)
is the sum of the quantity of prescriptions for all products i with the same brand–generic flag (b), molecule (m) and existing–exiting–entering status (e)
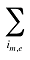 is the sum of quantity over all products i with the same molecule (m) and existing–exiting–entering status (e)
is the sum of quantity over all products i with the same molecule (m) and existing–exiting–entering status (e)
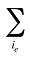 is the sum of quantity over all products i with the same existing–exiting–entering status (e)
is the sum of quantity over all products i with the same existing–exiting–entering status (e)
a(is,b,m,e,t) is the share of the quantity for product i over the sum of quantities for all products with the same brand–generic flag (b), molecule (m) and existing–exiting–entering status (e)
b(ib,m,e,t) is the share of the sum of quantities for products i with the same brand–generic flag (b), molecule (m) and existing–exiting–entering status (e) over the sum of quantities for all products with the same molecule (m) and existing–exiting–entering status (e)
d(im,e,t) is the share of the sum of quantities for products i with the same molecule (m) and existing–exiting–entering status (e) over the sum of quantities for all products with the same and existing–exiting–entering status(e)
l(ie,t) is the share of the sum of quantities for products i with the same existing–exiting–entering status (e) over the total quantity for all products in that period
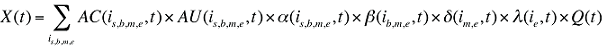
The change in total drug costs in period 1 over period 0 is:
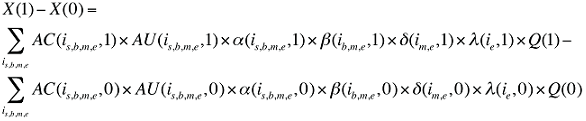
This formula can be written in the following form, isolating the following individual effects:
Formula 1. Cost Decomposition Formula – Drivers of Drug Costs

where
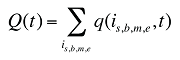
is calculated for all existing, exiting and entering drugs and q(is,b,m,e,t) is the number of prescriptions for product is,b,m,e in time period t
where
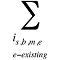 is the sum of all existing drugs
is the sum of all existing drugs
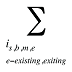 is the sum of all existing and exiting drugs, and
is the sum of all existing and exiting drugs, and
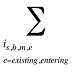 is the sum of all existing and entering drugs
is the sum of all existing and entering drugs
The first five effects in Formula 1 are calculated only for existing drugs, as they would take the value of zero for the exiting and entering drugs.
The Exiting Drug Effect and the Entering Drug Effect as seen in Formula 1 can be collapsed into one single Exiting–Entering Drug Effect, encompassing the two:
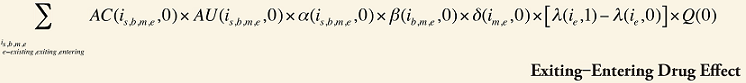
Note that the Exiting Drug Effect is limited to existing and exiting drugs. The term l(i,1) takes the value of 1 for Existing drugs and the value of 0 for Exiting drugs, as there are no Exiting drugs in time period 1. Similarly, the Entering Drug Effect is limited to the existing and entering drugs. The term l(i,1) takes the value of 1 for Existing drugs and the value of 0 for Entering drugs. Since the Entering drugs do not have values for time period 0, the values for time period 1 should be used instead. Appendix 9 provides an example of how the Existing, Exiting and the Entering Drug Effects are decomposed.
Note that in Formula 1, when a required value for one time period is not available, the value from the other time period should be used instead. This may happen, as the strengths or forms of some of the existing molecules may be used sporadically in one period or another.
The Drug Cross Effects are composed of 120 combined effects, as discussed in Appendix 5.
4.2 Drivers of Dispensing Fees
The drivers of dispensing fees, as described in Section 2.2, are as follows:
- Fee Effect
- Prescription Size Effect
- Drug Volume Effect
As a minimum, the following data elements are required for two time periods:
blank
| Molecule (active ingredient) |
|
| Strength and form4 |
Drug Attributes |
blank
| Dispensing fee expenditures |
|
| Units (number of tablets, capsules, etc.) |
Metrics |
| Number of prescriptions |
|
The metrics are aggregated at the attribute level, as opposed to the DIN level, in order to eliminate unnecessary detail, such as packaging sizes and manufacturer information.
Note that in the context of this analysis, a product refers to any combination of its attributes: molecule and strength and form.
The dispensing fee expenditure can be written as follows:
(10) F(t) = AF(t) × Q(t)
where
F(t) is the total dispensing fee expenditure in time period t
AF(t) is the average dispensing fee per prescription in time period t
Q(t) is the number of prescriptions in time period t
In turn, the number of prescriptions can be written as a function of the units dispensed:
(11)
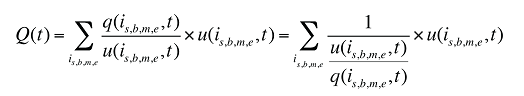
where
q(is,b,m,e,t) is the number of prescriptions for product is,b,m,e in time period t
u(is,b,m,e,t) is the number of units of product is,b,m,e in time period t
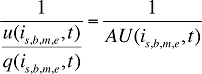
where
AU(is,b,m,e,t) is the average number of units per quantity of prescriptions for product is,b,m,e in time period t
This term is the inverse of the prescription size. The greater this term, the fewer the units of drug dispensed per prescription.
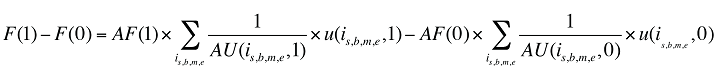
Formula 2. Cost Decomposition Formula – Drivers of Dispensing Fees
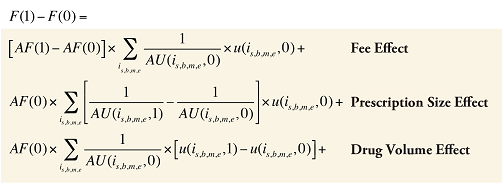
Fee Cross Effects
The Fee Cross Effects are composed of four combined effects, detailed in Appendix 7.
This methodology uses an average dispensing fee per prescription to determine the fee effect. Dispensing fees may vary across provinces, depending on the amount reimbursed by public plans, and may also vary depending on whether the pharmacy is located in an urban, rural or remote area.
Other professional fees related to medication management services and interventions may also be reported in the administrative data. This can include fees for prescription renewal, assessment and adaptation, therapeutic substitution, medication review, refusal to dispense/fill a prescription, etc. These fees need to be identified and removed from the analysis of the drivers of dispensing fees.5
Note that if 'day supply' information is available and reliably reported in the data, it may replace the 'unit' information when calculating the drivers of dispensing fees. In this case, the Prescription Size Effect and the Drug Volume Effect will become the Prescription Length Effect and a Volume Effect that reflects day supply information.
4.3 Demographic Effects of Drug Costs and Dispensing Fees
If relevant information is available, Demographic Effects can be isolated from the Volume Effects corresponding to the drug cost and dispensing fee components of the prescription drug expenditure. Demographic Effects encompass the following three effects (described in Section 2):
- Population Effect
- Aging Effect
- Gender Effect
Demographic Effects can be extracted if data on expenditures for the number of prescriptions and population size by age and gender grouping is available. The following data elements may be used for two time periods:
blank
| Age (5 or 10-year age bands recommended) |
Demographic Attributes |
| Gender |
|
blank
| Population size (number of patients, claimants, beneficiaries, etc.) |
|
| Drug cost (sales) or dispensing fee expenditures |
Metrics |
| Number of prescriptions |
|
The metrics need to be aggregated at the demographic level (age and gender). Age information may be available in the form of age bands; the more granular the age information, the more precise the calculation for the aging effect.
Demographic Effects for Drug Costs
At the population level, the drug costs or sales in a given time period for a population with a known age and gender distribution as well as size, can be written as the product of the average cost per prescription, average number of prescriptions per population and the number of patients in an age–gender grouping, summed up over all groups:
(12)
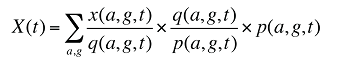
where
x(a,g,t) is the drug cost or sales for age group a and gender group g in time period t
q(a,g,t) is the number of prescriptions for age group a and gender group g in time period t
p(a,g,t) is the population in age group a and gender group g in time period t
This last term can be written as:
(13)
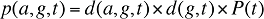
where
d(a,g,t) is the share of population in age group a and gender group g in total population of gender g in time period t
d(g,t) is the share of population in gender group g in total population in time period t
P(t) is the total population in time period t
(14)
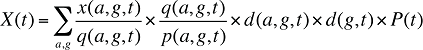
By keeping the average cost per prescription and the average number of prescriptions per population constant to the base period values, the Demographic Effects of drug costs can be isolated as follows:
Formula 3. Cost Decomposition Formula – Demographic Effects of Drug Costs
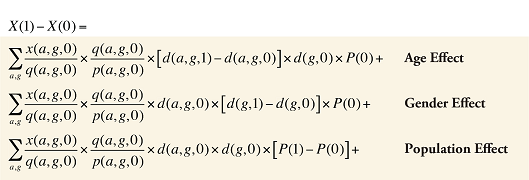
Demographic Cross Effects
The Demographic Cross Effects are composed of four combined effects, detailed in Appendix 6.
If the Demographic Effects of drug costs are calculated as described above, the Prescription Volume Effect in Formula 1 needs to be freed of Demographic Effects before the drug effects are determined. This is done by replacing Q(1) with QS(1), which is the quantity of prescriptions in time period 1 standardized for the same demographic profile as in time period 0. The demographic profile refers to the age (a), gender (g) and population size (P).
(15)
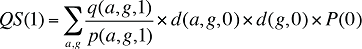
The Prescription Volume Effect calculated using QS(1) in Formula 1 is free of Demographic Effects, reflecting only the changes in the number of prescriptions for a population with the same age and gender distribution as well as size as in the base year.
Demographic Effects for Dispensing Fees
In a similar fashion, at a population level, the dispensing fee expenditures in a given time period for a population with a known age and gender distribution as well as size can be written as the product of the average fee per prescription, average number of prescriptions per population and the number of patients in an age–gender grouping, summed up over all groups:
(16)
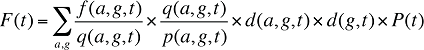
where
f(a,g,t) is the dispensing fee expenditure for age group a and gender group g in time period t
q(a,g,t) is the number of prescriptions for age group a and gender group g in time period t
p(a,g,t) is the population in age group a and gender group g in time period t
d(a,g,t) is the share of population in age group a and gender group g in total population of gender g in time period t
d(g,t) is the share of population in gender group g in total population in time period t
P(t) is the total population in time period t
By keeping the average fee per prescription and the average number of prescriptions per population constant to the base period values, the Demographic Effects of dispensing fee expenditures can be isolated as follows:
Formula 4. Cost Decomposition Formula – Demographic Effects of Dispensing Fee Expenditures
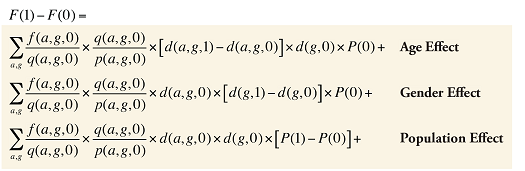
Demographic Cross Effects
The Demographic Cross Effects are composed of four combined effects, discussed in Appendix 6.
If the Demographic Effects of dispensing fee expenditures are calculated as described above, the Drug Volume Effect in Formula 2 needs to be freed of Demographic Effects by replacing u(is,b,m,e,1) with us(is,b,m,e,1), which is the number of units standardized for the same demographic profile as in time period 0. This is calculated based on the standardized number of prescriptions, as follows:
(17)
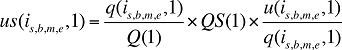
where
q(is,b,m,e,1) is the number of prescriptions for product is,b,m,e in time period 1
u(is,b,m,e,1) is the number of units (physical quantities) for product is,b,m,e in time period 1
Q(1) is the total number of prescriptions in time period 1
QS(1) is the number of prescriptions in time period 1 standardized for the same demographic profile as in time period 0, as derived in equation (15). The demographic profile refers to the age (a), gender (g) and population size (P).
(18)
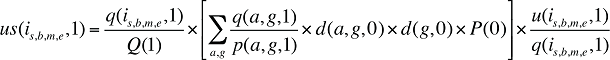
u(is,b,m,e,1) in Formula 2 is then replaced with us(is,b,m,e,1) as derived in equation (18). The Drug Volume Effect from Formula 2 calculated using us(is,b,m,e,1) is free of Demographic Effects, reflecting only the changes in the quantity of drugs dispensed in a population with the same age and gender distribution as well as size as in the base year.
4.4 Drivers of Plan-Paid Share of Costs
Some administrative databases may also contain information on the portion of prescription drug expenditures reimbursed by drug plans (public or private), as well as the portion paid by the beneficiary.
In any given time period, this relation can be expressed as:
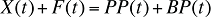
where
X(t) is the total drug cost in time period t
F(t) is the total dispensing fee expenditure in time period t
PP(t) is the total plan-paid amount reimbursed in time period t
BP(t) is the total beneficiary-paid amount in time period t
The plan-paid amount can be calculated as:
(19)
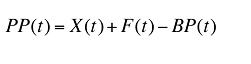
The change in the plan-paid amount over two time periods can be written as:
(20)
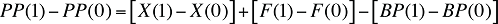
As the above equation implies, the drivers of the plan-paid amount are simply the sum of the drivers of drug cost and dispensing fees, from which the drivers of beneficiary-paid amounts are subtracted.
Assuming that there is demographic information available, the beneficiary-paid amount can be written in a manner similar to equation (14):
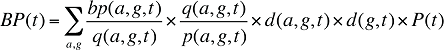
where
bp(a,g,t) is the beneficiary-paid amount for age group a and gender group g in time period t
Formula 5. Cost Decomposition Formula – Drivers of Beneficiary-Paid Amounts

Beneficiary-Paid Cross Effects
The Beneficiary-Paid Cross Effects are detailed in Appendix 8.
The individual effects in equation (20) can be calculated as detailed in Formulas 1–4, capturing the Price, Volume, Drug-Mix and Demographic Effects, etc. Some effects, such as the Volume and Demographic Effects from the drug cost and dispensing fee components, will partially cancel the corresponding effects from the beneficiary-paid component. The net effect will be the driver of the plan-paid component.
A simpler approach would be to decompose the plan-paid change in the same way as the beneficiary-paid amount in Formula 5, replacing the Beneficiary-Paid per Prescription Effect with the Plan-Paid per Prescription Effect. This will be a broad effect encompassing Price and Drug-Mix Effects and even some of the Volume Effects such as the Prescription Size Effect and the Strength–Form Effect.
The approach proposed in this section, explains the changes in plan-paid amounts through the drivers of drug cost, dispensing fees and beneficiary-paid amounts. This approach captures changes in plan design (e.g., changes in the deductible-copayment structure) indirectly through the beneficiary-paid component. Determining the precise impact of plan design changes on plan-paid expenditures requires the development of a different model.
3 The strength and form should only be combined for products that are oral solids (tablets, capsules, extended release formulations, etc.). Other formulations (injectable, inhalers, patches, etc.) should be considered as distinct products.
4 The strength and form should only be combined for products that are oral solids (tablets, capsules, extended release formulations, etc.). Other formulations (injectable, inhalers, patches, etc.) should be considered as distinct products.
5 If the purpose of the analysis is to determine the drivers of expenditures related to professional services in general, and the data is available, then these professional fees may be retained for analysis. They can be aggregated under types of fees (e.g., dispensing fees, medication review fees, therapeutic substitution fees, etc.), and the cost driver model can be adjusted to capture a fee-type effect. Note that for medication management services and interventions, the type of fee and amount reimbursed varies by province.
5. Adjustments and Enhancements to the Methodology
The cost driver approach proposed in this study is not limited to the effects discussed, nor does it have to encompass all of these effects. The methodology may be adapted depending upon the data availability and research requirements. This section provides options for reducing, expanding or redefining the effects that can be captured through the cost decomposition methodology.
Cost driver analyses are not limited to total drug sales or program expenditures. Using the standard methodology, it is possible to conduct specialized analyses of expenditure for particular groups of drugs (e.g., therapeutic classes) or segments of the population (e.g., drug plans or their specific subgroups).
Furthermore, the methodology is not limited to trend analyses of changes in sales or expenditures over time, but can also be employed in cross-jurisdictional analyses or international comparisons that break down the sources of differences in drug sales or expenditures.
5.1 Reducing the Number of Effects
The following elements may be removed from or replaced in the proposed methodology:
Demographic Effects
One, some or all of the Demographic Effects may be removed from the analysis. If all Demographic Effects are removed, Formulas 1 and 2 can be used without Formula 3 and 4, respectively. If one or two of the demographic effects are removed, Formulas 1 and 2 would be used in conjunction with a modified version of Formulas 3 and 4.
Price and Generic Substitution Effects
If the drug type information available does not distinguish between brand-name and generic products, these two effects may be collapsed into one: a price effect that includes generic substitution.
In this case, the required attributes would be the molecule, strength and form. The average price for each drug would be determined at strength and form level and would reflect the prices and the corresponding weights of both the brand-name and the generic drugs. In the absence of brand versus generic information, the factor b(i,k) would be removed from Formula 1, and the Generic Substitution Effect would be folded into the Price Effect.
Prescription Volume Effect
If information on the number of prescriptions is not available, the use of physical units as a standalone measure of quantity in drug cost driver models would have two implications:
- The Prescription Size Effect and the Prescription Volume Effect would be folded into the Drug Volume Effect.
- The number of physical units would have to be used to determine the each product's share of the volume. However, physical units are generally not cumulative across drugs, given that drugs come in different strengths (e.g., 5, 10, 500 mg) and formulations (e.g., oral solids, injectable, ointments, patches). This would impact the Drug-Mix Effect, as the share of drugs that are reported as multiple units (in the case of oral solids) or as single units (in the case of patches, or injectables, etc.) could be skewed. This limitation is mitigated if the analysis is conducted only on one formulation, e.g., oral solids.
If physical units are used as the measure of quantity, the factor AU(is,b,m,e,t) is removed from Formula 1, and the factor q(is,b,m,e,t) will become the quantity expressed in units for drug is,b,m,e in time period t.
Of course, if the number of prescriptions is not known, an analysis of the drivers of dispensing fees cannot be conducted.
Physical Units
If information on the number of physical units is not available, the use of the number of prescriptions as a standalone measure of quantity in cost driver models for both drug costs and dispensing fees would have two implications:
- In the drivers of drug costs model, the Price Effect will be replaced by an Average Cost per Prescription Effect, which would be a very broad measure incorporating the Price Effect and Prescription Size Effect. Consequently, equation (7) would be replaced by the collapsed formula below, with a corresponding revision to Formula 1.
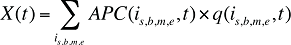
where APC(is,b,m,e,t) is the average cost per prescription for drug is,b,m,e in time period t.
- In the drivers of dispensing fees model, the Prescription Size Effect and the Drug Volume Effect would be collapsed into a single Prescription Volume Effect. In this model, Formula 2 would be based on equation (10) without the further decomposition displayed in equation (11).
Exiting and Entering Drug Effects
These two individual effects may be collapsed into one encompassing Exiting–Entering Drug Effect as previously discussed.
5.2 Expanding the Number of Effects
Therapeutic Effect
The Existing Drug Effect can further be decomposed by therapeutic class and even subclass. This can be done by adding another component to the product description: therapeutic class c.
Consequently, equation (9) can be revised by adding another factor e(ic,e,t), as follows:
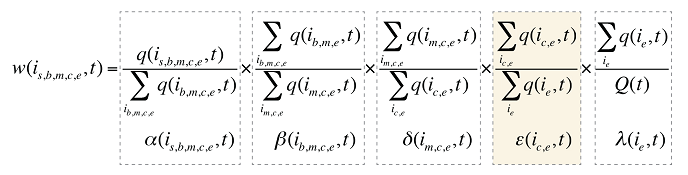
where
e(ic,e,t) is the share of the sum of the quantity of all products i with the same therapeutic class (c) and existing–exiting–entering status (e) over the sum of the quantity for all products with the same and existing–exiting–entering status (e).
A Subclass Effect may be added to the Therapeutic Effect in a similar fashion. Formula 1 can be revised accordingly.
Patented versus Non-Patented Effect
The drugs can further be classified into patented and non-patented drugs. This can be done by adding another term to equation (9), in a similar manner as above.
Treatment Intensity Effect
If the data allows for the accurate identification of treatment length (days) for the quantity of drugs utilized, the methodology may be enhanced to capture a Treatment Intensity Effect.
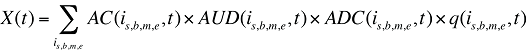
where
X(t) is the total drug cost in time period t
AC(is,b,m,e,t) is the average cost per unit for drug is,b,m,e in time period t
AUD(is,b,m,e,t) is the average number of units per day of treatment for drug is,b,m,e in time period t
ADC(is,b,m,e,t) is the average number of days of treatment per prescription for drug is,b,m,e in time period t
q(is,b,m,e,t) is the quantity of prescriptions for drug is,b,m,e in time period t
Formula 1 can be revised by adding a new effect that captures the changes in the number of units dispensed per day (treatment intensity) and by altering the Prescription Size Effect to capture the changes in the number of days of treatment dispensed per prescription instead of the number of physical units dispensed per prescription.
5.3 Redefining the Effects
Single-source versus multi-source drugs (SSD–MSD)
The SSD–MSD Effect can replace the Generic Substitution Effect. This can be accomplished by simply assigning a single-source or multi-source designation to a drug instead of the brand or generic type.
The SSD would mainly refer to brand products, whereas the MSD would refer to all molecules that have multiple trade names available, whether brand-name or generic products. This means that once generic copies are available, the brand-name product will switch status from SSD to MSD.
The SSD–MSD effect would differ from the Generic Substitution Effect, as it would only capture the effect of drugs moving from a single-source to multi-source status, thus reflecting only the initial impact of generic substitution. Moreover, the Price Effect will also be different, as it will capture not only the true price effect but also the changes from a brand to a generic in a multi-source category. This will reflect the remainder of the generic substitution impact.
Note that depending on the addition or reduction in the number of effects, the cross effects formulas need to be revised as required.
6. Limitations
The proposed drug expenditure decomposition methodology has a number of limitations, which are discussed in this section.
The methodology decomposes prescription drug expenditures into the driving factors that can be extracted from administrative databases. However, due to the limitations of the available data, some important drivers may not be captured (e.g., disease prevalence, prescribing practices, and socio-economic factors).
Although the effects are generically referred to as drivers, they may not be drivers per se, but rather markers for real drivers. The Prescription Volume Effect and the Existing Drug Effect are good examples. They may be driven, in turn, by changes in the incidence rates for diseases, physician prescribing practices, treatment guidelines, reimbursement policies, etc.
Given that the cost driver analysis provides high-level results for the market analyzed, it is mainly used to point toward the areas of growth. This information can be used to conduct further analyses in specific areas of interest.
Cost decomposition is a very complex analysis, and quality assurance and validation is required to ensure that the methodology is correctly applied. Furthermore, the application of this methodology requires an understanding of the advantages and limitations of the data, awareness of the aspects that affect growth specific to the data analyzed, and knowledge of the relevant research focus.
This study is conceptually based on the Laspeyres decomposition approach, which is essentially a forward-looking approach. However, there is more than one method of conducting cost decomposition analyses, including the Paasche and Fisher's Ideal decompositions. These price and quantity indices have their own limitations. Therefore the choice of approach should depend on the focus of the research and how the results are going to be used.
7. Conclusion
A cost driver analysis can be an effective tool in understanding drug cost pressures and allows policy makers and researchers to analyze past trends and predict future outcomes. Furthermore, the methodology can also be employed in cross-jurisdictional analyses or international comparisons that break down the sources of differences in drug sales or expenditures.
This study identifies the major cost drivers of prescription drug expenditures and provides researchers with the formulas required to conduct cost driver analyses.
The proposed methodology can be adjusted and enhanced based on data availability and the purpose and analytical depth of a particular research study. Using the standard methodology, it is possible to conduct specialized analyses of expenditure in particular therapeutic classes or market segments. Also, the methodology can be used in cross-jurisdictional analyses that break down the sources of differences in per capita expenditure.
Note that the methodology described in this report proposes one way of conducting cost driver analysis. The process described is intended to assist researchers in understanding the mechanics of the cost decomposition methodology and in designing their own methodology in line with their analytical interests.
8. References
Berndt ER, Cutler DM, Frank RG, Griliches Z, Newhouse JP, Triplett JE. 2000. Medical Care Prices and Output. In: Handbook of Health Economics. Edited by: Culyer AJ, Newhouse JP. Amsterdam: Elsevier Science B.V.
CIHI. 2011. Health Care Cost Drivers: The Facts. Ottawa: Canadian Institute for Health Information. https://secure.cihi.ca/free_products/health_care_cost_drivers_the_facts_en.pdf
(Accessed Dec. 1, 2013)
CIHI. 2012. Drivers of Prescription Drug Spending in Canada. Ottawa: Canadian Institute for Health Information. http://www.cihi.ca/CIHI-ext-portal/pdf/internet/DRUG_SPEND_DRIVERS_EN (Accessed Dec. 1, 2013)
CIHI. 2013. Drug Expenditure in Canada, 1985 to 2012. Ottawa: Canadian Institute for Health Information. https://secure.cihi.ca/free_products/Drug_Expenditure_2013_EN.pdf
(Accessed Dec. 1, 2013)
CBO. 2008. Technological Change and the Growth of Health Care Spending. Washington, D.C.: Congressional Budget Office. http://www.cbo.gov/ftpdocs/89xx/doc8947/MainText.3.1.shtml
Diewert W.E. 2001. The Consumer Price Index and the Index Number Theory: A Survey. Vancouver: Vancouver School of Economics, the University of British Columbia, Discussion Paper 01-02.
Gerdtham UG, Lundin D. 2004. Why did drug spending increase during the 1990s?. PharmacoEconomics. 22(1):29–42.
Morgan SG. 2002. Quantifying Components of Drug Expenditure Inflation: The British Columbia Seniors' Drug Benefit Plan. Health Services Research. 37(5):1243–1266.
Morgan SG. 2004. Drug Spending in Canada: Recent Trends and Causes. Medical Care. 42(7):635–642.
Morgan SG. 2005. Drug Expenditure Trends in the Canadian Provinces: Magnitude and Causes from 1998 to 2004. Healthcare Policy. 1(1): 85–99. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2585243/ (Accessed Dec. 1, 2013)
PMPRB. 2004. The Pharmaceutical Trends: Non-Insured Health Benefits (NIHB) Pharmacy Program 1999–2000 to 2001–2002. Ottawa: Patented Medicine Prices Review Board.
PMPRB. 2006. Pharmaceutical Trends Overview Report: Alberta, Saskatchewan, Manitoba, Ontario, New Brunswick, Nova Scotia, and First Nations and Inuit Health Branch of Health Canada 1997–1998 to 2003–2004. Ottawa: Patented Medicine Prices Review Board.
PMPRB. 2010. Use of the World Health Organization Defined Daily Dose in Canadian Drug Utilization and Cost Analyses. Ottawa: Patented Medicine Prices Review Board. http://www.pmprb-cepmb.gc.ca/CMFiles/Publications/Analytical%20Studies/NPDUIS-WHO-DDD-e.pdf (Accessed Dec. 1, 2013)
PMPRB. 2011. Public Drug Plan Dispensing Fees: A Cost-Driver Analysis, 2001/02 to 2007/08. Ottawa: Patented Medicine Prices Review Board. http://www.pmprb-cepmb.gc.ca/CMFiles/Publications/Analytical%20Studies/NPDUIS-DispensingFees-e-sept30.pdf (Accessed Dec. 1, 2013)
United Nations Statistics Division. 2008. Updated System of National Accounts (SNA): Chapter 15: Price and volume measures. New York: United Nations. http://unstats.un.org/unsd/statcom/doc08/SNA-Chapter15.pdf (Accessed Dec. 1, 2013)
Appendix 1: Laspeyres Decomposition
The Laspeyres decomposition discussed in Section 3.2 describes the simple case of one product for which the expenditure is a function of two factors: price and quantity. Real-world cost driver analysis typically encompasses many products for which the drug expenditure is a function of multiple factors. This type of framework is discussed in detail in this appendix.
The Laspeyers approach is a forward-looking approach. It should be employed to answer the following type of question:
How much higher is the expenditure this year simply because of higher prices?
This approach should be employed when the price and the quantity effects need to reflect the actual overall increase in price and quantity, respectively. In this case, a residual cross effect will be present, corresponding to the interaction between the price and quantity effects. If any sort of attribution of the cross effect is attempted, the price effect will not equal the price increase, and similarly, the quantity effect will not equal the increase in quantity.
Extension to Many Products
This extension requires that we now think of P and Q as ordered lists of matching values, that is, vectors of associated prices and quantities. Working with vectors makes computation more complicated but uses the same basic framework: in particular, the analysis set out in equations (1)–(6) is still valid.6
In the single price–quantity case, a positive price (or quantity) effect implies that the price (or quantity) must have risen between the base period and current period. Things are more complicated when there are multiple prices and quantities. In this case, it is possible to have a positive price (or quantity) effect if some, or even most prices (or quantities), fell between the base period and current period. To see how this can occur, note that the price effect in equation (6) can be written:
(A1) MP = [P(1) – P(0)]Q(0)
Thus (7) can be re-written as7:
(A2) MP = [w1D1 + w2D2 … + wNDN]X(0)
where Di is the change in the price of product i expressed as a percentage of its base-period price, and wi is the share of the base-period expenditure for product i. If D1, D2 … DN contains both positive and negative values, it is impossible to determine whether MP will be positive or negative without actually calculating the sum on the right-hand side of equation (8). However, in general MP will tend to be positive (negative) if price increases coincide with large (small) expenditure shares and price decreases with small (large) expenditure shares. A similar result holds for the quantity effect.
In the case of multiple products, the positive or negative value of the cross effect cannot be determined without actually doing the calculations, even if the analyst knows the direction of the price and quantity effects. The cross effect has the form and properties of a statistical correlation between changes in prices and quantities. Thus, if large price changes coincide with large quantity changes of the same (opposite) direction, then the cross effect will tend to be large and positive (negative). On the other hand, if large changes in prices and quantities do not coincide (for example, if large price increases are restricted to one subset of products and large quantity changes to a completely different subset), then the cross effect will tend to be small even in data containing many large price and quantity changes.
The Extension to Multiple Factors
Suppose that the variable of interest X is determined by a set of N factors Z1,Z2 … ZN according to a known functional relationship:
(A3) X = F(Z1, Z2 … ZN)
This implies:
(A4.1) X(0) = F[Z1(0), Z2(0) … ZN(0)]
(A4.2) X(1) = F[Z1(1), Z2(1) … ZN(1)]
Our goal is to set out a Laspeyres decomposition that accounts for expenditure change in full by assigning shares of that change to the N factors and their various combinations. By analogy to (6), such a decomposition will include N first-order (“direct”) effects, defined by
(A5) M1(i) = F[Z1(0) … Zi(1) … ZN(0)]
– F[Z1(0) … Zi(0) … ZN(0)] i = 1… N
In keeping with the Laspeyres approach, each first-order effect M1,i is obtained as the change in X that would have occurred if only factor Zi changed.
Second-order (“double cross”) effects are defined by
(A6) M2(i,j) = F[Z1(0) … Zi(1) … Zj(1) … ZN(0)]
– F[Z1(0) … Zi(0) … Zj(0) … ZN(0)]
– [M1(i) + M1(j)] i = 1 … N, j = 1 … N
Each second-order effect is calculated as the change in X that would have occurred had only factors Zi and Zj changed, net of each factor's direct effect. Note that by removing direct effects in the right-hand side of (A6), we obtain an expression that truly represents the expenditure impact of interactions between the changes in Zi and Zj. This expression describes a component of expenditure change that is incremental to the components attributable to the direct effects of Zi and Zj, meaning it can be added to the direct effects without double-counting.
To produce a full set of second-order effects, equation (A6) must be applied to every possible distinct pair of factors. There will be N(N – 1)/2 such pairs, and hence, the same number of second-order effects to compute.8
Third-order (“triple cross”) effects are defined by
(A7) M3(i,j,k) = F[Z1(0) … Zi(1) … Zj(1) … ZK(1) … ZN(0)]
– F[Z1(0) … Zi(0) … Zj(0) … ZK(0) … ZN(0)]
– [M2(i,j) + M2(i,k) + M2(j,k)]
– [M1(i) + M1(j) + M1(k)] i = 1 … N, j = 1 … N, k = 1 … N
That is, each third-order effect is calculated as the change in X that would have occurred if only factors Zi, Zj and Zk changed, net of each factor's direct effect and the three second-order effects for Zi, Zj and Zk are implicated. To produce a full set of third-order effects, equation (A7) must be applied to every possible distinct trio of factors. There will be N(N – 1)(N – 2)/6 such trios, and hence, the same number of third-order effects.
Higher-order effects can be constructed in a fashion similar to (13) until we reach the Nth-order effect:
(A8) MN (1,2, … N) = F[Z1(1), Z2(1) … ZN(1)]
- F[Z1(0), Z2(0) … ZN(0)]
- yN-1
where yN-1 represents the sum of all effects of all orders 1 through (N – 1). Using equations (A4.1) and (A4.2) in (A8) gives:
(A9) X(1) – X(0) = MN (1,2 … N) + yN-1
The right-hand side of equation (A9) includes all effects of all orders, that is, all direct and cross effects, computed in accordance with the foregoing procedure. The sum of these effects equals the change in X, as required.
The decomposition outlined above will generate 2N – 1 distinct effects.9 This implies that the number of effects to be computed increases exponentially with the number of factors included in the analysis, doubling (approximately) with each additional factor. Most of this increase occurs because of the proliferation of cross effects: adding one more factor to a pre-existing set of N generates a single new direct effect but 2N – 1 additional cross effects.
6 It is important to understand that the right-hand side of (6) will still return a single value even if P and Q are vectors. A special form of multiplication applies in the case of vectors. Let A and B be two vectors each containing V values. In particular, let A = [a1,a2…aV] and B = [b1,b2…bV]. In this case the product of A and B is defined as the sum of the products of their corresponding matching values, that is, AB = a1b1 + a2b2 …+ aVbV. This result is known as the “inner product” of A and B.
7 The price effect in (6) can be written in inner product form as:
MP = Q1(0)[P1(1) – P1(0)] + Q2(0)[P2(1) – P2(0)]… + QV(0)[PV(1) – PV(0)]
Multiplying and dividing each term by the corresponding base-period price allows us to write:
MP = P1(0)Q1(0) {[P1(1) – P1(0)]/P1(0)} + P2(0)Q2(0){[P2(1) – P2(0)]/P2(0)}…
+ PV(0)QV(0){[PV(1) – PV(0)]/PV(0)}
Multiplying and dividing each term by base-period price expenditure gives:
MP = [P1(0)Q1(0)/X(0)] {[P1(1) – P1(0)]/P1(0)}X(0)
+ [P2(0)Q2(0)/X(0)]{[P2(1) – P2(0)]/P2(0)}X(0)…
+ [PV(0)QV(0)/X(0)]{[PV(1) – PV(0)]/PV(0)}X(0)
The expression [Pi(0)Qi(0)/X(0)] is product i's share of base-period expenditure, while {[Pi(1) – Pi(0)]/Pi(0)} is the proportionate change in product i's price.
8 A well-known formula gives the number of distinct subsets of Q distinct elements that can be formed from a larger set of N distinct elements. This formula is C(Q,N) = N!/[Q!(N – Q)!], where I! = I(I – 1)(I – 2)… for any positive integer I. If Q = 2, we have C(2,N) = N!/[2!(N – 2)!] = [N(N – 1)]/2.
9 Each Zi(t) can take on a value of either Zi(0) or Zi(1). This means the N-tuple [Z1(t),Z2(t)…ZN(t)] can have 2N distinct values. Each of these is associated with a distinct direct or cross effect except for [Z1(0),Z2(0)…ZN(0)], which defines base-period expenditure. Hence, there are 2N – 1 distinct effects to compute in performing the generalized Laspeyres decomposition.
Appendix 2: Paasche Decomposition
The Laspeyres approach evaluates the impacts of changes in factors at the base-period values of all other factors. In contrast, the Paasche approach evaluates the impact of each factor on drug expenditure by holding all other factors at their current-period values.
Therefore, the Paasche approach is backward-looking. It should be employed to answer the question:
How much lower would the expenditure have been this year at last year's prices?
This approach is less likely to be used as a stand-alone tool in cost driver analysis due to its hypothetical nature. However, it may be used in conjunction with the Laspeyres approach in the Fisher ideal decomposition.
Consider the elementary “P times Q” case once again. The Paasche decomposition begins with the observation that
(A10.1) P(0) = P(1) – [P(1) – P(0)]
(A10.2) Q(0) = Q(1) – [Q(1) – Q(0)]
Substituting (10.1) and (10.2) into (1) gives
(A11) X(1) – X(0) = P(0)Q(0) – {P(1) – [P(1) – P(0)]}{Q(1) – [Q(1) – Q(0)]}
The right-hand-side of (11) simplifies to:
(A12) X(1) – X(0) = [P(1) – P(0)]Q(1) + P(1)[Q(1) – Q(0)] – [P(1) – P(0)][Q(1) – Q(0)]
The three terms on the right-hand side of equation (A12) constitute the Paasche-type of decomposition of expenditure change:
The first term on the right-hand side of equation (A12) is a Paasche-type price index, expressed as a difference rather than in ratio form. It measures the impact of changes in price on expenditure, evaluated at current-period quantities.
The second term is a Paasche-type quantity index, expressed as a difference rather than in ratio form. It measures the impact of changes in quantities on expenditure, evaluated at current-period prices.
The third term is the Paasche cross effect. It measures the impact of interactions between the changes in prices and quantities.
Comparing equation (6) and equation (A12) reveals that the Paasche cross effect is the negation of the Laspeyres cross effect. Because the Paasche approach evaluates the direct price and quantity effects at current-period values, each of these effects already includes the impact of interactions between price and quantity changes. In this case, a correction is required to avoid double-counting the impact of price-quantity interactions. The Paasche cross effect provides this correction.
Appendix 3: Fisher Ideal Decomposition
The Laspeyres and Paasche price and quantity effects are equally valid but answer different questions, as one is forward-looking and the other is backward-looking. Consequently, they would give different estimates of drivers. Moreover, neither of these two approaches result in the full attribution of expenditure growth among the individual effects, due to the existence of the cross effects.
The use of symmetric averages has been proposed as a way to addressing the limitations of the Laspeyres and Paasche indexes. These symmetric averages may be the arithmetic mean or the geometric mean of the Laspeyres and Paasche indexes, referred to as the Fisher ideal index (Diewert 2001). In particular, the Fisher approach has been used in other published studies on cost drivers (Morgan 2002, 2004, 2005). The Fisher ideal price index is considered to be the “best” evenly weighted average of the two price indices, as it is a homogeneous symmetric average and satisfies the time reversal test (Diewert 2001).
The Fisher ideal approach is the full-attribution of expenditure approach. It is a hybrid between the Laspeyres and Paasche approaches, in that it combines the forward-looking and the backward-looking approaches and results in a full attribution of the cross effects across the individual effects. The same outcome may be achieved by equally distributing the Laspeyres cross effects across the individual contributing factors.
The Fisher ideal approach should be used when the analysis requires that the expenditures are fully attributed to the individual effects, acknowledging that each effect captures the interaction with all the other effects. Moreover, this approach should only be employed when the equal distribution of the cross effects is considered appropriate.
The principle of the Fisher ideal index is transferable to the approach proposed in this paper, namely, by taking a simple of average of the right-hand sides of the Laspeyres (6) and Paasche (A12) effects detailed above. Since both of these expressions equal the change in expenditure, we obtain
(A13) X(1) – X(0) = [P(1) – P(0)][(1/2)Q(1) + (1/2)Q(0)]
+ [(1/2)P(1)+(1/2)P(0)][Q(1) – Q(0)]
The right-hand side of (A13) gives the Fisher ideal approach to the decomposition for the two-factor case. The first term on the right-hand side of (A13) is the price effect, measuring the impact of changes in price on expenditure, evaluated at the mid-point between the base-period and current-period quantities. The second term is the quantity effect, measuring the impact of changes in quantity on expenditure, evaluated at the mid-point between base-period and current-period prices.
Note that equation (A13) does not include a cross term. To see why, note that
(A14.1) (1/2)P(1) + (1/2)P(0) = P(0) + (1/2)[P(1) – P(0)]
(A14.2) (1/2)Q(1) + (1/2)Q(0) = Q(0) + (1/2)[Q(1) – Q(0)]
Substituting equations (A14.1) and (A14.2) into (A15) gives
(A15) X(1) – X(0) = {[P(1) – P(0)][Q(0) + (1/2)[P(1) – P(0)][Q(1) – Q(0)]}
+ {[P(0)[Q(1) – Q(0)] + (1/2)[P(1) – P(0)][Q(1) – Q(0)]}
The two terms in braces on the right-hand-side of (A15) are the price and quantity effects, respectively. Comparing these to the Laspeyres price, quantity and cross effects in (6) reveals that the Fisher ideal approach obtains its price and quantity effects by adding one half of the Laspeyres cross effect to each of the Laspeyres price and quantity effects. In a similar fashion, the Fisher ideal approach can be shown to divide the Paasche cross effect equally between the Paasche price and quantity effects. This approach is referred to in this paper as the Fisher ideal decomposition.
Appendix 4: Full Attribution of Cross Effects
Given the limitations discussed in Section 3.3 relating to the full attribution of cross effects, the recommendation is to report the cross effects as a separate total. In this case, the individual effects will be reported as described in Section 4, and the portion of the expenditure resulting from cross effects will be reported separately.
If, however, the full attribution of the cross effects is desired, this may be achieved by following the algorithm outlined in this appendix, which provides the framework for equally distributing the cross effects across the individual effects. This approach is similar to the Fisher ideal decomposition.
For example, consider the following three-factor model: expenditure as the product of price, quantity-per-claimant and claimant population. In this case, there will be four Laspeyres cross effects to compute: three double effects involving changes in two of the three factors, as well as a triple effect involving changes in all three factors.
The Fisher ideal decomposition approach requires that each double effect is divided equally between the two factors contributing to the change. Similarly, the triple effect should be divided equally among all three contributing factors. Expressed algebraically, the Fisher ideal price effect IP in this case would be given by:
(A16) IP = [P(1) – P(0)]Q(0)Z(0)
+ 1/2[P(1) – P(0)][Q(1) – Q(0)]Z(0)
+ 1/2[P(1) – P(0)]Q(0)[Z(1) – Z(0)]
+ 1/3[P(1) – P(0)][Q(1) – Q(0)][Z(1) – Z(0)]
where Z represents the number of claimants and Q should now be interpreted as the quantity-per-claimant. Expressions representing the Fisher ideal effects Z and Q would be constructed in a similar way to equation (A16). By adding these expressions to (A16), it is clear that the three Fisher ideal effects account for all seven of the Laspeyres direct and cross effects.
Although more challenging, it is possible to produce a Fisher ideal decomposition when there are four or more factors to consider. The key is consistent application of the principal of equal division: where a cross effect involves changes in Q factors, each of the factors should be assigned an equal share of that cross-effect. An algorithm for this process would proceed as follows.
Step 1. Calculate all direct and cross effects using the generalized Laspeyres approach outlined above.
Step 2. Inspect each double cross effect. Assign one half of each value to the two factors contributing to the change.
Step 3. Inspect each triple cross effect. Assign one third of each value to the three factors contributing to the change.
Step 4. Continue Steps 2 and Step 3 for each remaining cross effect, assigning equal shares of the effect to each of the contributing factors. This process will end with one Nth of the single Nth-order cross effect being assigned to each of the factors considered in the analysis.
Step 5. Take the sum of each factor's direct effect and the shares of all cross effects assigned in Steps 2 through 4. This will produce a complete decomposition of expenditure change into N elements, each of which is uniquely associated with one of the N factors considered in the analysis.
Appendix 5: Drug Cross Effects
As previously noted, the decomposition methodology divides the change in overall expenditure into a variety of direct and cross effects. The number of effects will depend on the number of factors considered in the analysis. If there are N factors, there will be 2N – 1 distinct effects in total, of which N will be direct effects and 2N – (N + 1) will be cross effects. It is possible to identify N – 1 levels of cross effects, involving interactions of two factors, three factors and so forth. The number of distinct level-Q cross effects will be the number of distinct combinations of Q elements that can be formed from an original set of N elements: this is given by the well-known formula C(N,Q) = N!/[Q!(N – Q)!)], where X! = X(X – 1)(X – 2) … 1.
As an example, consider a decomposition that attributes expenditure change to three factors. Since N = 3 in this case, there will be 23 – 1 = 7 effects in total, of which 3 will be direct effects and 23 – (3 + 1) = 4 will be cross effects. There will be N – 1 = 2 levels of cross effects – level 2 (“double cross effects”) involving interactions between two factors and level 3 (“triple cross-effects”) involving the interaction of all three factors: more exactly, there will be C(3,2) = 3 level 2 cross effects and C(3,3) = 1 level 3 cross effects.
Note that the number of distinct effects increases exponentially with the number of factors included in the decomposition, doubling (approximately) with the addition of each new factor. This increase is mainly due to the proliferation of cross effects: adding one more factor to a pre-existing set of N generates only a single new direct effect but 2N – 1 additional cross effects.
While Formula 1 decomposes eight effects, it is actually based on seven factors. This is because the Exiting and Entering Effects in Formula 1 can also be considered as one Exiting–Entering Drug Effect.
Therefore, the Drug Cross Effects are composed of 120 combined effects as described below. Note that if the cost decomposition methodology is modified to account for additional or fewer factors, the number of cross effects will also need to be revised accordingly.
21 Double Cross Effects: 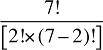 , such as:
, such as:
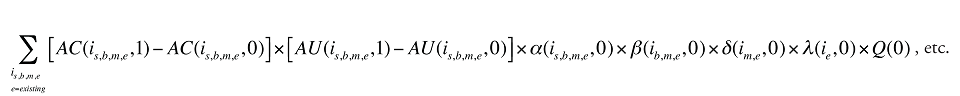 ,
,
35 Triple Cross Effects: 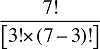 , such as:
, such as:
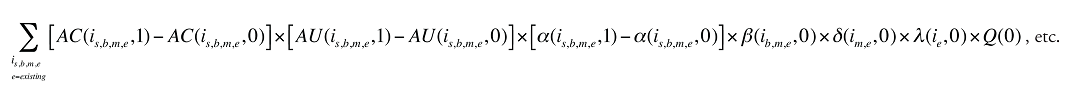
35 Quadruple Cross Effects: 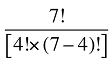 , such as:
, such as:
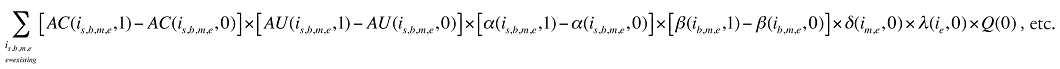
21 Pentuple Cross Effects: 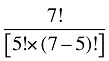 , such as:
, such as:
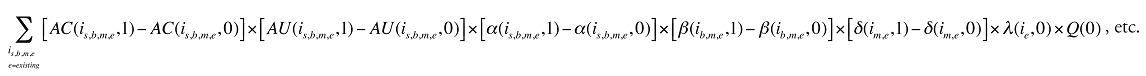
7 Hextuple Cross Effects: 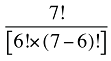 , such as:
, such as:
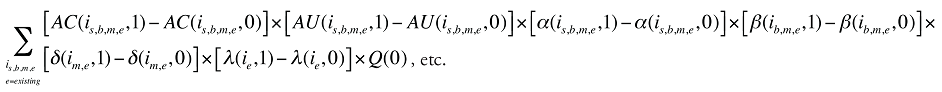
1 Septuple Cross Effect: 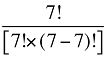 , namely:
, namely:
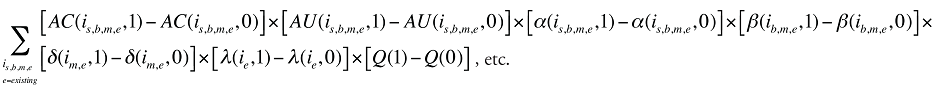
Appendix 6: Demographic Cross Effects
The Demographic Cross Effects for the Drug Cost component of prescription drug expenditures are composed of four combined effects as detailed in the formulas below.
3 Double Cross Effects: 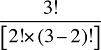
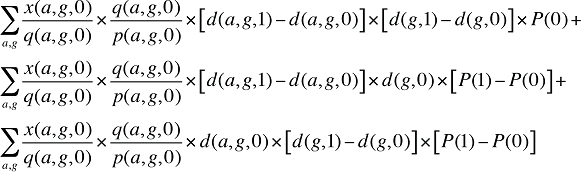
1 Triple Cross Effect: 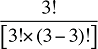
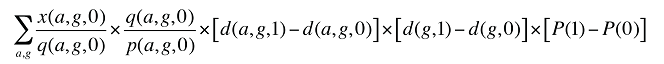
In a similar fashion, the Demographic Cross Effects for the Dispensing Fee component of prescription drug expenditures can be determined by replacing the drug cost x(a,g,t) in the formulas above with the dispensing fee expenditures f(a,g,t).
Appendix 7: Fee Cross Effects
The Fee Cross Effects are composed of four combined effects as detailed in the following equations.
3 Double Cross Effects: 
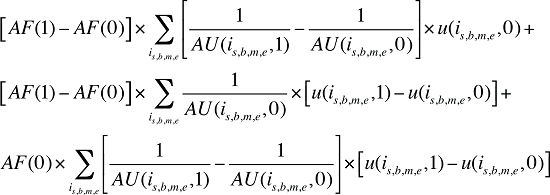
1 Triple Cross Effect: 
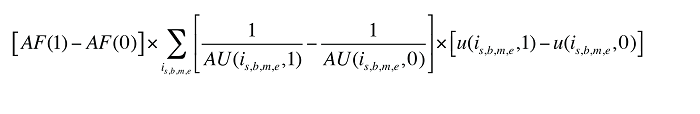
Appendix 8: Beneficiary-Paid Cross Effects
The Beneficiary-Paid Cross Effects are detailed below.
10 Double Cross Effects: 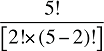 , such as
, such as
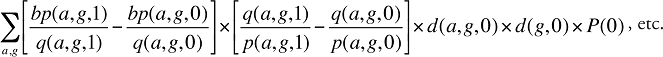
10 Triple Cross Effects: 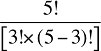 , such as
, such as
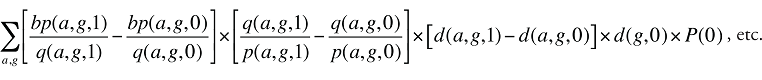
5 Quadruple Cross Effects: 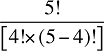 , such as
, such as
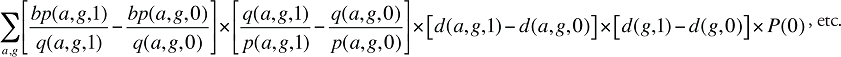
1 Pentuple Cross Effect: 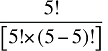 , such as
, such as
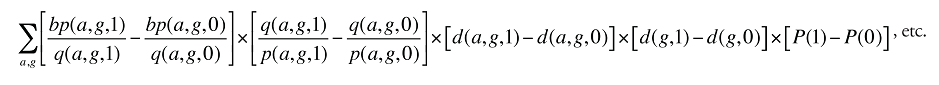
Appendix 9: Simplified Example of Cost Driver Analysis: Existing, Exiting and Entering Drug Effects
This appendix provides a simplified example of how the drug cost or sales can be decomposed, with a focus on the Existing, Exiting and the Entering Drug Effects discussed in Section 4.1
Consider the example of four molecules – A,B,C and D – with various drug types, prices, quantities and corresponding sales and costs, as indicated in Table A9.1.
Table A9.1. Hypothetical example of a four-product market: price times quantity
blank
| Drug type |
Active molecule |
Price |
Quantity |
Total costs (sales) |
| ie |
im |
p(im,e,0) |
p(im,e,1) |
q(im,e,0) |
q(im,e,1) |
x(im,e,0) |
x(im,e,1) |
| Entering |
A |
|
$20 |
– |
33 |
– |
$660 |
| Existing |
B |
$10 |
$12 |
40 |
33 |
$400 |
$396 |
| Existing |
C |
$15 |
$17 |
50 |
44 |
$750 |
$748 |
| Exiting |
D |
$5 |
|
10 |
– |
$50 |
– |
|
Total |
|
Q(0) = 100 |
Q(1) = 110 |
X(0) = $1,200 |
X(1) = $1,804 |
| DQuantity = 10 (10%) |
DCost = $604 (50.3%) |
The expenditure in any given time period can be written as:
(A17) 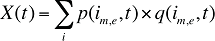
where
im,e is the product of a specific molecule (m) and existing-exiting-entering status (e)
t is a constant corresponding to one of the two time periods analyzed
X(t) is the total drug expenditures or sales in time period t
p(im,e,t) is the average cost or price per physical unit for product im,e in time period t
q(im,e,t) is the product's im,e share of total volume (expressed in prescriptions) in time period t
Note that q(im,e,t) = w(im,e,t) X Q(t)
then A17 becomes:
(A18) 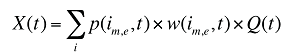
where
w(im,e,t) is the product's im,e share of total volume (expressed in prescriptions) in time period t
Q(t) is the total volume of prescriptions in time period t
Table A9.1 can be written as Table A9.2.
Table A9.2. Hypothetical example of a four-product market: the use of shares
blank
| Drug type |
Molecule |
Price |
Shares |
Total Quantity |
Total costs (sales) |
| ie |
im |
p(im,e,0) |
p(im,e,1) |
w(im,e,0) |
w(im,e,1) |
Q(0) |
Q(1) |
x(im,e,0) |
x(im,e,1) |
| Entering |
A |
|
$20 |
– |
30% |
100 |
110 |
– |
$660 |
| Existing |
B |
$10 |
$12 |
40% |
30% |
100 |
110 |
$400 |
$396 |
| Existing |
C |
$15 |
$17 |
50% |
40% |
100 |
110 |
$50 |
$748 |
| Exiting |
D |
$5 |
|
10% |
– |
100 |
110 |
$750 |
– |
|
Total |
|
100%
|
100%
|
|
X(0) = $1,200 |
X(1) = $1,804 |
|
DCost = $604 (50.3%) |
Note that this is a simplified version of equation (7) in Section 4.1. Equation A17 assumes that quantity is expressed in units rather than claims and considers that products do not have a particular strength-form combination (s) or a brand-generic flag (b), or that these characteristics are irrelevant.
As described in Section 4.1, each individual share w(im,e,t) can be decomposed into multiple shares, as follows:
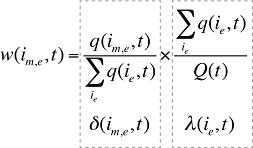
where
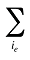 is the sum of the quantity of all products i with the same existing-exiting-entering status (e).
is the sum of the quantity of all products i with the same existing-exiting-entering status (e).
d(im,e,t) is the share of the quantity for product i with the same molecule (m) and existing-exiting-entering status (e) over the sum of quantities for all products with the same existing-exiting-entering status (e).
l(ie,t) is the share of the sum of quantities for the products i with the same existing-exiting-entering status (e) over the total quantity for all products in that period.
Formula (A18) can be rewritten as:
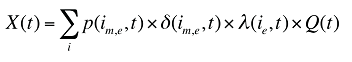
As in Formula 1, the Existing-Exiting-Entering Drug Effect can further be decomposed as follows:
(A19)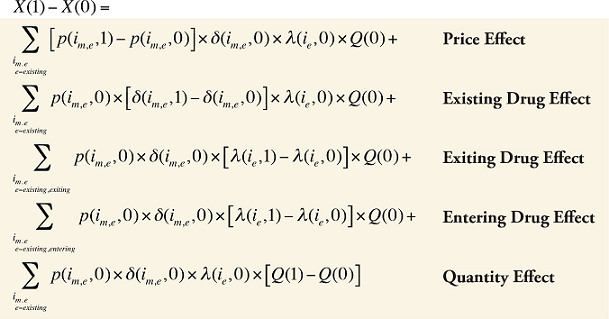
where
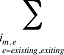 is the sum over all existing and exiting drugs, and
is the sum over all existing and exiting drugs, and
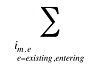 is the sum over all existing and entering drugs
is the sum over all existing and entering drugs
For the example provided in Table A9.1 and Table A9.2, the shares of the products can be further broken down based on the existing, exiting and entering drug types as in Table A9.3.
Table A9.3. Hypothetical example of a four-product market: the use of shares
blank
| Drug type |
Molecule |
Price |
Shares for
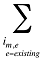
|
Shares for
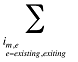 |
Shares for
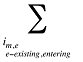 |
Total quantity |
Total costs (sales) |
| ie |
im |
P(0) |
P(1) |
d(im,e,0) |
d(im,e,1) |
l(ie,0) |
l(ie,1) |
l(ie,0) |
l(ie,1) |
Q(0) |
Q(1) |
x(im,e,0) |
x(im,e,1) |
| Entering |
A |
|
$20 |
|
100% |
|
|
|
30% |
100 |
110 |
– |
$660 |
| Existing |
B |
$10 |
$12 |
44% |
43% |
90% |
100% |
100% |
70% |
100 |
110 |
$400 |
$396 |
| Existing |
C |
$15 |
$17 |
56% |
57% |
90% |
100% |
100% |
70% |
100 |
110 |
$750 |
$748 |
| Exiting |
D |
$5 |
|
100% |
|
10% |
|
|
|
100 |
110 |
$50 |
– |
|
Total |
|
X(1)=$1,200 |
X(0)=$1,804 |
|
DCost = $604 (50.3%) |
Note that the Exiting Drug Effect is limited to the existing and exiting drugs 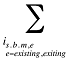 .The term l(i,1) takes the value of 1 for Existing Drugs and the value of 0 for Exiting Drugs, as there are no Exiting Drugs in time period 1.
.The term l(i,1) takes the value of 1 for Existing Drugs and the value of 0 for Exiting Drugs, as there are no Exiting Drugs in time period 1.
Also note that the Entering Drug Effect is limited to the existing and entering drugs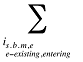 . The term l(i,0) takes the value of 1 for Existing Drugs and the value of 0 for Entering Drugs, as there are no Entering Drugs in time period 0.
. The term l(i,0) takes the value of 1 for Existing Drugs and the value of 0 for Entering Drugs, as there are no Entering Drugs in time period 0.
As a validation step, the values for total sales or costs highlighted in orange in Tables A9.1–A9.3 should remain the same throughout the decomposition process.
The values in Table A9.3 can be easily used to calculate (A19). The results are provided in Table A9.4.
Table A9.4. Individual effects of the cost driver analysis
blank
| Drug type ie |
Molecule im |
Price Effect |
Existing Drug Effect |
Exiting Drug Effect |
Entering Drug Effect |
Quantity Effect |
| Entering |
A |
– |
– |
– |
$600 |
– |
| Existing |
B |
$80 |
-$16 |
$44 |
-$129 |
$40 |
| Existing |
C |
$100 |
$24 |
$83 |
-$257 |
$75 |
| Exiting |
D |
– |
– |
-$50 |
– |
$5 |
|
Total
(% of D Cost) |
$180 (15.0%) |
$8 (0.7%) |
$78 (6.5%) |
$214 (17.9%) |
$120 (10.0%) |
|
Total |
|
$600 (50.0%) |
|
Also as a validation step, the result for the Quantity Effect as a percentage of the DCost (10%) should be the same as the change in the quantity of drugs over the two periods as reported in Table A9.1.
The difference between the sum of all effects in Table A9.4 of $600 (or 50.0% of the X(0)) and the difference in sales or costs between the two periods of $604 (or 50.0% of the X(0)) as reported in Tables A9.1–A9.3 is due to the cross effects, which are detailed below in equation (A20). For simplicity, they are calculated based on equation (A18).
(A20)
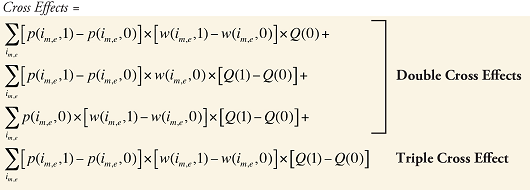
The cross-effect formulas applied to the example yield the following results:
Table A9.5. Cross effects of the cost driver analysis
blank
| Drug type ie |
Molecule im |
Cross effect 1 |
Cross effect 2 |
Cross effect 3 |
Cross effect 4 |
Total |
| Entering |
A |
– |
– |
$60 |
– |
$60 |
| Existing |
B |
-$20 |
$8 |
-$10 |
-$2 |
-$24 |
| Existing |
C |
-$20 |
$10 |
-$15 |
-$2 |
-$27 |
| Exiting |
D |
– |
– |
-$5 |
– |
-$5 |
|
-$40 |
$18 |
$30 |
-$4 |
|
|
Total (% of D Cost) |
|
$4.00 (0.3%) |
Note that the sum of the cross effects in Table A9.4 is $4 (0.3% over X(0)), which added to the total of the individual effects in Table A9.5 of $600 (or 50.0% of the X(0)) yields the exact total sales or cost differentials between the two periods of $604 (or 50.3% of the X(0)), as calculated in Tables A9.1–A9.3.
The example provided in this section explains the cost driver analysis in simple terms. The same idea can be applied to larger data sets and more effects, as discussed in the body of this report.
This example also explains how the cross effects may be distributed if the full attribution of the cost across individual effects is desired.
For instance, the cross effect 2 of $18 in Table A9.5 would be divided in two. Half of it would go to the Price Effect and the other half to the Quantity Effect in Table A9.4. Similarly, the triple cross effect would be divided in three, with 1/3 being assigned to the Price Effect, Existing Effect and Quantity Effect in Table A9.4.
Note that the Quantity Effect in this case will not only reflect the increase of 10% in the quantity, but will also reflect the interaction with the other factors: while the quantity has increased, the increase includes new, more expensive drugs as well as higher prices for existing drugs.